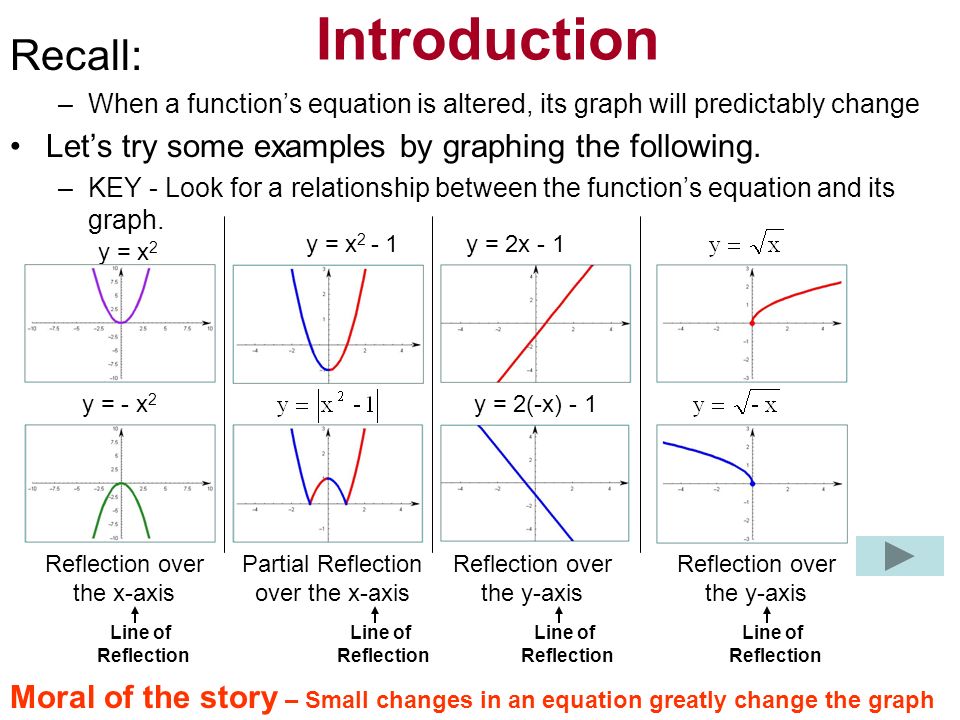
In addition to shifting, compressing, and stretching a graph, we can also reflect it about the x axis or the y axis When we multiply the parent function f (x) = bx f (x) = b x by –1, we get a reflection about the x axis When we multiply the input by –1, we get a reflection about the y axisThis video demonstrates how to reflect a figure over the xaxis on the coordinate plane The video shows how to use the rule and use the counting methodThis video explains to graph graph reflections across the xaxis and yaxis in the form a*f(b(xc))d This video looks at how the sign of a and b affect th
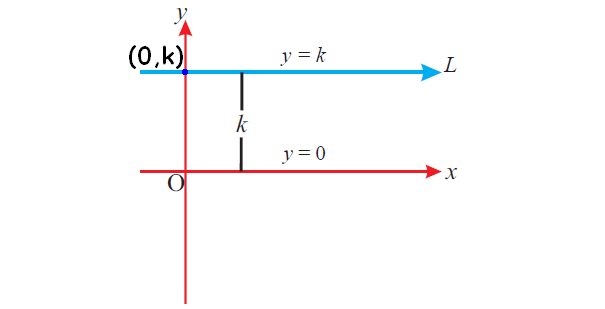
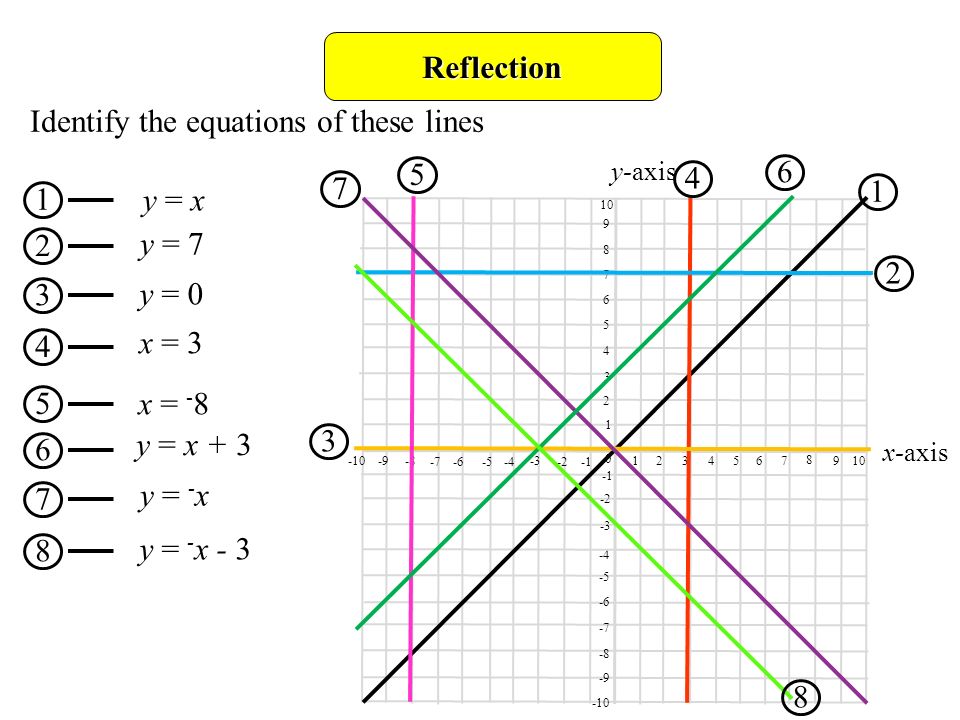
Equation Of A Line Parallel To X Axis
Reflection over x axis vs y axis equation
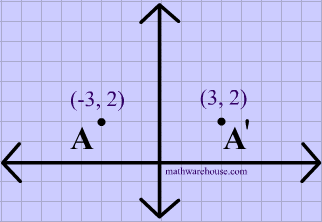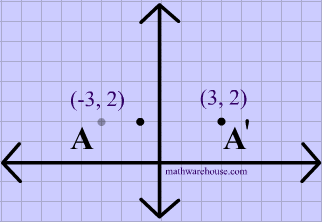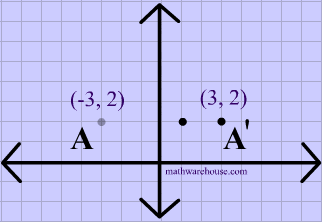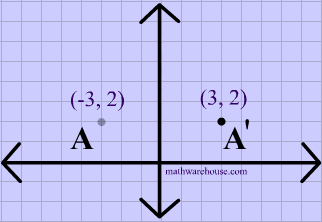
Reflection over x axis vs y axis equation-Selina Concise Mathematics Part II Solutions for Class 10 Mathematics ICSE, 12 Reflection (In xaxis, yaxis, x=a, y=a and the origin ;Each xvalue of the preimage is the same as the imageOnly the yvalues have changed and become opposite of the preimage




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
From this expression it is clear that the all the values of y coordinate axis are changed by their negative values and the values of x coordinate axis are unchanged Therefore, the final result will show a flip over along the x axis If there is a point (x, y) on a plane, then its vertical reflection can be denoted by the point (x, y) To reflect it over the yaxis, the reflection will be in quadrant 2, still above the xaxis, but now left of the yaxis The distance the reflection is from the yaxis is the same as the original point is from the yaxis The reflection of (5, 5) over the yaxis is (5, 5) To reflect any point over the yaxis, replace the xcoordinate with theThe point negative 8 comma 5 is reflected across the yaxis plot negative 8 comma 5 and its reflection across the yaxis so first let's plot negative 8 comma 5 so its xcoordinate is negative 8 so I'll just use this one right over here so the xcoordinate is negative 8 and the ycoordinate is 5 so I'll go up 5 so the ycoordinate is 5 right over here you see negative 8 and 5 we've gone 8 to
The following diagram shows function transformations that involves reflections across the xaxis and yaxis Scroll down the page for more examples and solutions on how to reflect functions or graphs This video explains how to graph reflections across the xaxis and yaxis in the form a*f (b (xc))d This video looks at how the sign of a and3 Reflect the graph of the parent function latexf\left(x\right)={\mathrm{log}}_{b}\left(x\right)/latex about the xaxis 3 Reflect the graph of the parent function latexf\left(x\right)={\mathrm{log}}_{b}\left(x\right)/latex about the yaxis 4 Draw a smooth curve through the points 4 Draw a smooth curve through the points 5Du vill reflektera (7, 3) i yaxeln Låt denna punkt vara P (7, 3) och låt punkten att hitta vara Q (x, y) När punkten reflekteras i yaxeln förblir punktens ykoordinat densamma Tecknet på xkoordinat förändras Punkten P är i den tredje kvadranten så att reflektionen i yaxeln kommer att vara i den fjärde kvadranten
Invariant Points) All the solutions of Reflection (In xaxis, yaxis, x=a, y=a and the origin ;The line y = 15x – 2 is reflected in the line y = 1 What is the equation of the image?Polar graph polar equation symmetry reflection x axis symmetric about the x axis 303 videos Symmetry of Polar Graphs Precalculus Polar Coordinates and Complex Numbers How to determine if the graph of a polar equation is symmetric about the xaxis




Reflection Mathbitsnotebook A1 Ccss Math




Equation Of A Line Parallel To X Axis
Você deseja refletir (7, 3) no eixo y Seja este ponto P (7, 3) e o ponto a encontrar seja Q (x, y) Agora, quando o ponto é refletido no eixo y, a coordenada y do ponto permanece a mesma O sinal da coordenada x muda O ponto P está no terceiro quadrante, portanto sua reflexão noHow would this graph differ from the graph of cycle number vs number of radioactive nuclei?Apply the rule to find the vertices of the image Since there is a reflection across the xaxis, we have to multiply each ycoordinate by 1 That is, (x, y) > (x, y) Step 2



Reflect Function About Y Axis F X Expii




What Is The Difference Between Y F X And Y F X Quora
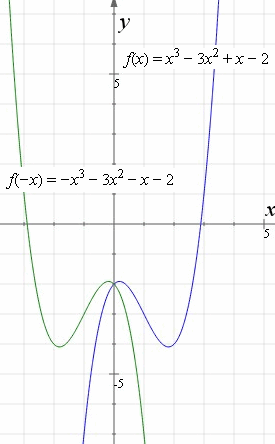
Use the checkboxes to investigate how the triangle is reflected in either the xaxis or the yaxis Then answer the questions below Use what you learned from the investigation above to answer the following questions 1) If the point (2, 3) is reflected over the xaxis what is the new point?Reflexão sobre o eixo x vs eixo y resposta 1 A3 Oi!Reflections and Rotations We can also reflect the graph of a function over the x axis (y = 0), the y axis (x = 0), or the line y = x Making the output negative reflects the graph over the x axis, or the line y = 0 Here are the graphs of y = f (x) and y = f (x)



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download
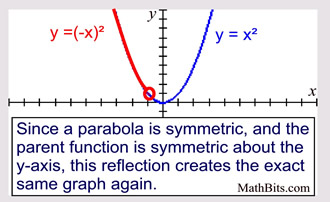
Let y = f (x) be a function In the above function, if we want to do reflection through the yaxis, x has to be replaced by x and we get the new function y = f (x) The graph of y = f (x) can be obtained by reflecting the graph of y = f (x) through the yaxisPoint Z is located at $$ (2,3) $$ , what are the coordinates of its image $$ Z'$$ after a reflection over the xaxis Show Answer Remember to reflect over the xaxis , just flip the sign of the yAnd also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the x axis nor the y axis



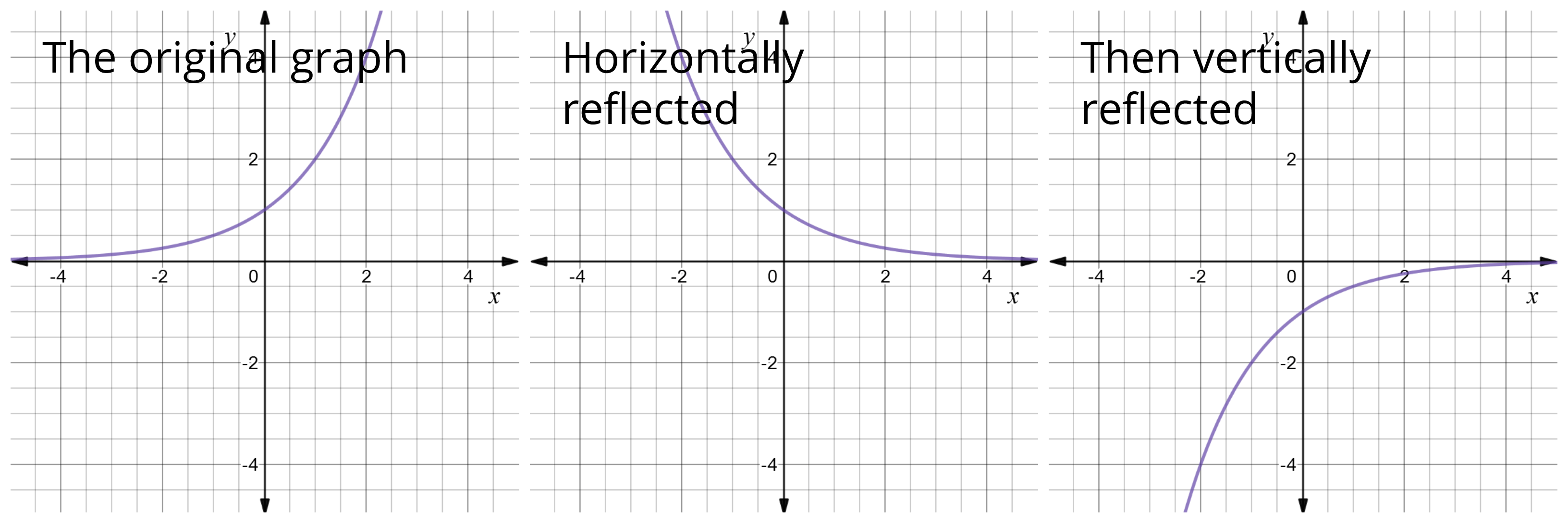
Transforming Exponential Functions




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
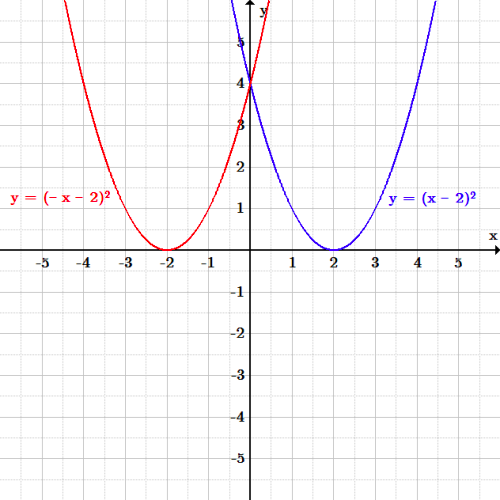
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the xFrom the equation, you can see that the horizontal shift will be to the left 10 units and there will be a reflection over the yaxis Therefore, reflect the graph of over the yaxis and then shift (move) the reflected graph left 10 units The point (1, 0) is shifted to (1, 0) with the reflection and then to (1 10, 0) or ( 11, 0) SupposeA vertical reflection is given by the equation latexy = f(x)/latex and results in the curve being "reflected" across the xaxis A horizontal reflection is given by the equation latexy = f(x)/latex and results in the curve being "reflected" across the yaxis Key Terms Reflection A mirror image of a function across a given line
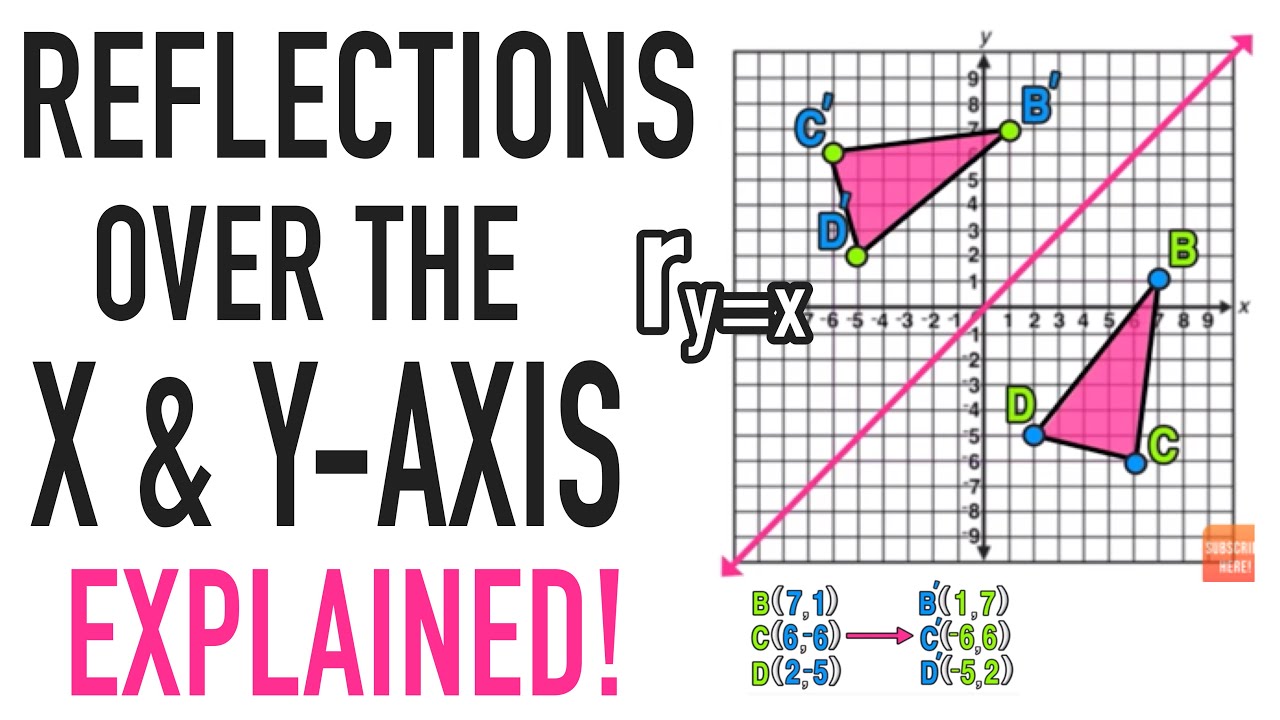



Reflections Over The X Axis And Y Axis Explained Youtube



Transformations Of Functions Mathbitsnotebook A1 Ccss Math
To reflect the absolute value function over the xaxis, we simply put a negative sign before the symbol (in this case the absolute value bars) Our new equation would be y = Ix3I Check the graphs in your calculator, they should look like a mirror image of each other, reflected over the xaxis Now try reflecting reciprocal y = 1/x 4As you can see, the graph of y 2 (x) is in fact the base graph g(x) reflected across the xaxis Reflections Across the yAxis You can visualize a reflection across the yaxis by imagining the graph that would result from folding the base graph along the yaxis Symbolically, we define reflections across the yaxis as followsAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators




Function Transformations Dilation Mathmaine



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line
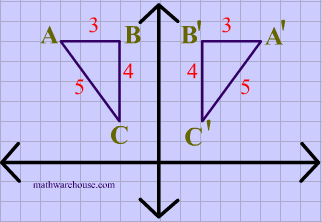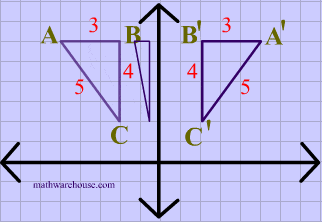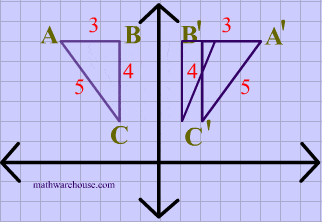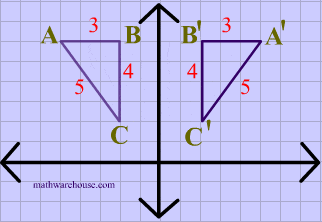
X and Y Axes Two of the most common reflections are when a figure is reflected across either the x or yaxis The triangle below has been reflected across the xaxisNotice the change that occured to the corresponding ordered pair;P (x) = a (x)^2 b (x) c = ax^2 bx c 11K viewsAnother transformation that can be applied to a function is a reflection over the x – or y axis A vertical reflection reflects a graph vertically across the x axis, while a horizontal reflection reflects a graph horizontally across the y axis The reflections are shown in Figure 9 Figure 9
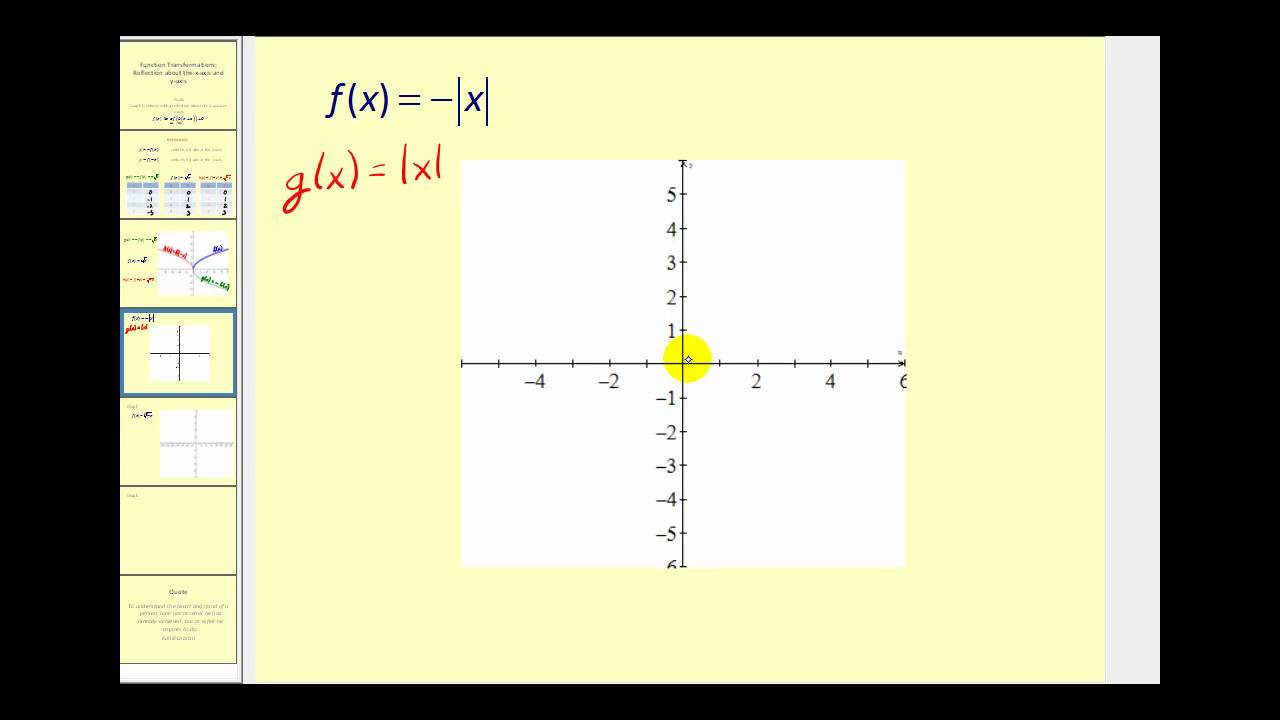



Function Transformations Reflections Across The X Axis And Y Axis Youtube




How To Reflect Quadratic Equations Video Lesson Transcript Study Com
Reflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =You can also negate the value depending on the line of reflection where the xvalue is negated if the reflection is over the yaxis and the yvalue is negated if the reflection is over the xaxis Either way, the answer is the same thingAnother transformation that can be applied to a function is a reflection over the x x – or y y axis A vertical reflection reflects a graph vertically across the x x axis, while a horizontal reflection reflects a graph horizontally across the y y axis The reflections are shown in Figure 9 Vertical and horizontal reflections of a function



Assignment 2 Transforming Parabolas
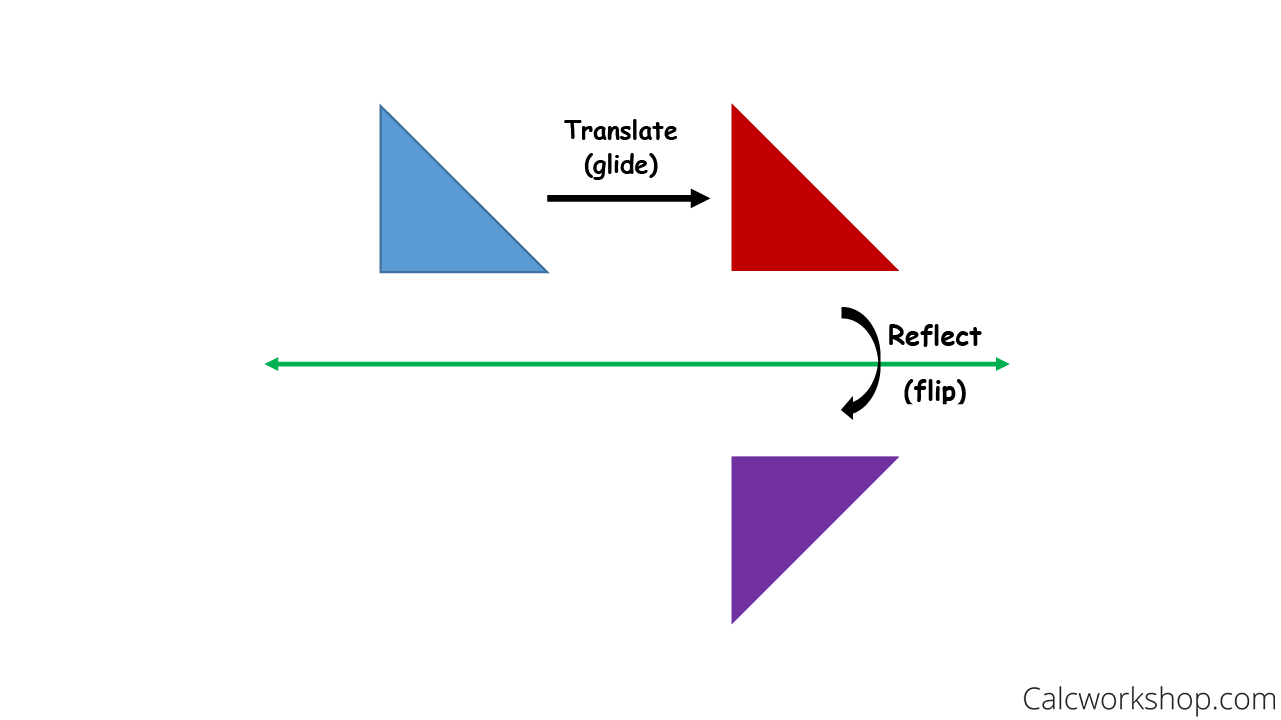



Reflection Rules How To W 25 Step By Step Examples
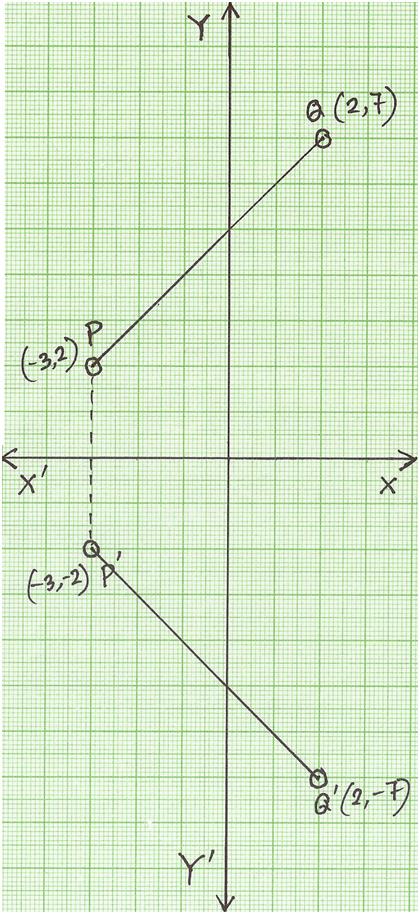
The answer from question (1) is reflected in the line x = 4 What is the equation of the image?Reflect (3,9) over the y axis (3,9) Reflect (3,9) over the y axis YOU MIGHT ALSO LIKE ChildPugh ID Exam 4 21 Terms Claire_Hodge58 Dairy Cow Unified Scorecard 27 Terms Quizlet Live One step equations with integers Part 1 12 Terms Laurel_Lochner One Step Equations (6th Grade) 23 Terms Nick_Houk Adding Integers Terms The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)
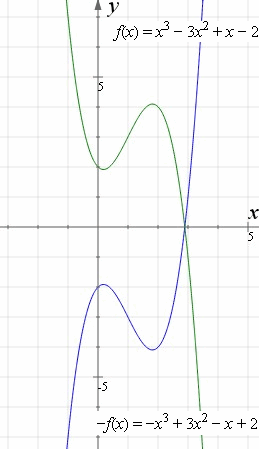



How To Reflect A Graph Through The X Axis Y Axis Or Origin
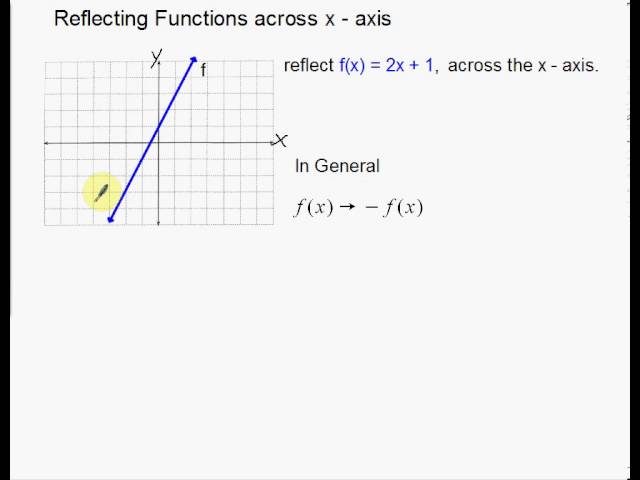



Linear Reflections Across X And Y Axis Youtube
Check all that apply The graph would flip over The graph would be logarithmic instead of exponential The xaxis would change title and values The yaxis would change title and valuesThe shapes are the same The graph of is a reflection over the xaxis of the graph of Fold the graph of over the xaxis so that it would be superimposed on the graph of Every point on the graph of would be shifted up or down twice it's distance from the xaxis For example, the point (a, 8) is located 8 units up from the xaxis How has the graph changed if the equation is fx21 Reflection in the x axis A 12 B 35 and C 71 By counting the units we know that point A is located two units above the xaxis Reflection over the xaxis A reflection over the xaxis can be seen in the picture below in which point A is reflected to its image A
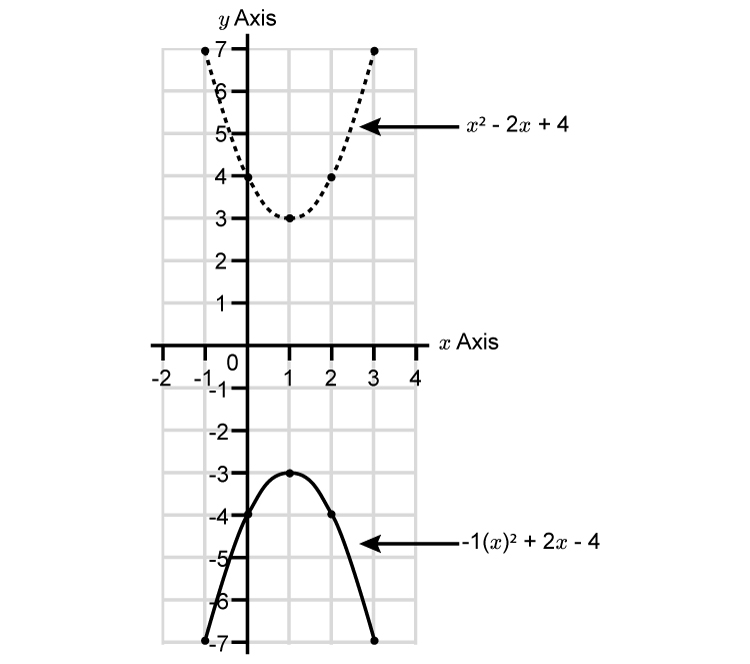



Reflecting More Difficult Parabolas Mammoth Memory Maths



Assignment 11
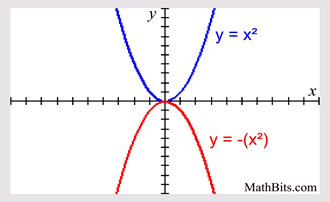
A reflection across xaxis is nothing but folding or flipping an object over the x axis The original object is called the preimage, and the reflection is called the image If the preimage is labeled as ABC, then t he image is labeled using a prime symbol, such as A'B'C' An object and its reflection have the same shape and size, but the figures face in opposite directionsThe effect of the reflection was to change the major axis of the ellipse from horizontal to vertical When the line of reflection is the xaxis, the ycoordinates will be equal, but the xcoordinates will be opposites x' = x and y' = yReflection across the xaxis y = − f ( x) y = f (x) y = − f ( x) The concept behind the reflections about the xaxis is basically the same as the reflections about the yaxis The only difference is that, rather than the yaxis, the points are reflected from above the xaxis to below the xaxis, and vice versa Basic Concepts
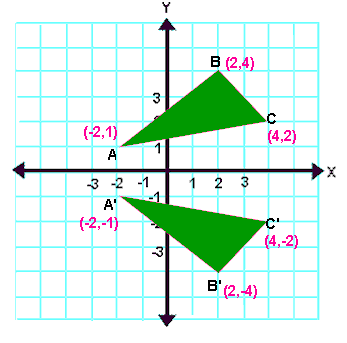



Reflection Transformation Matrix



1
You have two choices to reflect either reflect across the yaxis or the yaxis In either case you need the negative of the opposite value In other words if you want to reflect across the xaxis then you need the opposite of the y value VicevThus for y = f ( x), the reflection about the line y = x is accomplished by x = f ( y) For example, the reflection about the line y = x for y = x 2 is the equation x = y 2 Hope it helps If the curve is complicated, you can just take particular, interesting points and switch the coordinatesY axis) Reflection over line y=x or y=Reflection over line y=x or y=xx Reflection over y=x Point (x,y) reflects to point (y,x) Reflection over line y=x



Search Q Vertical Compression Tbm Isch
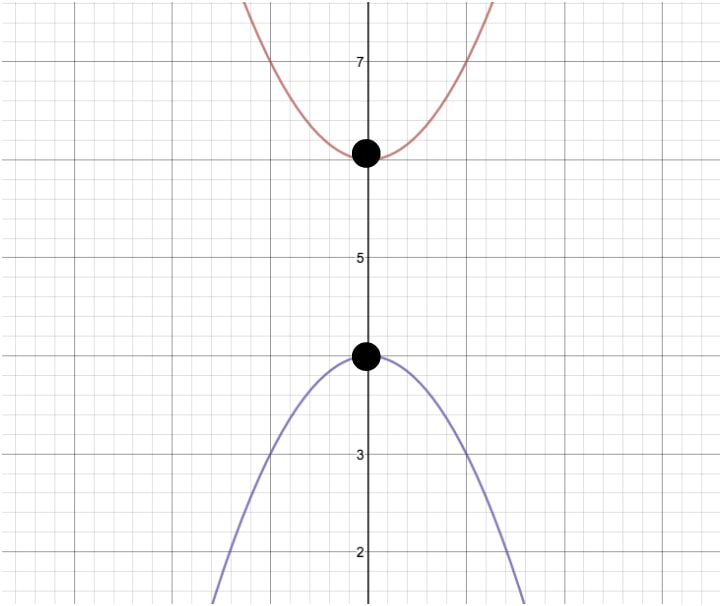



How To Reflect A Graph Through The X Axis Studypug
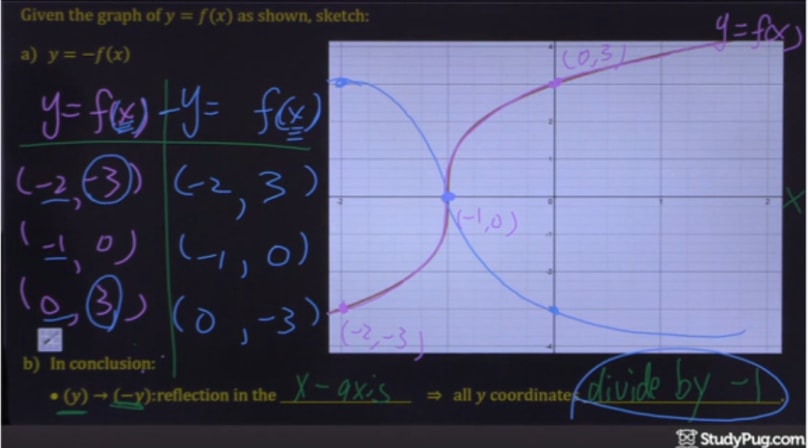
Remember that when a point P (x, y) of the coordinate plane is reflected in the y axis, it becomes the point Q (x, y) and when reflected in x axis, it becomes P' (x, y) Therefore the quadratic p (x) = ax^2 bx c (a not zero) when reflected in y axis it becomes ;For this type of reflection, all you have to do is switch the x and y values if a point is (4,2), then the inverse is (2,4) If you begin with a function y=sqrt (x), there are many different lines you could reflect this function across, but only reflecting over y=x will give you the inverse of the function y=xThe best way to practice drawing reflections over y axis is to do an example problem Example Given the graph of y = f (x) y=f(x) y = f (x) as shown, sketch y = f (− x) y = f(x) y = f (− x) Remember, the only step we have to do before plotting the f(x) reflection is simply divide the xcoordinates of easytodetermine points on our



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
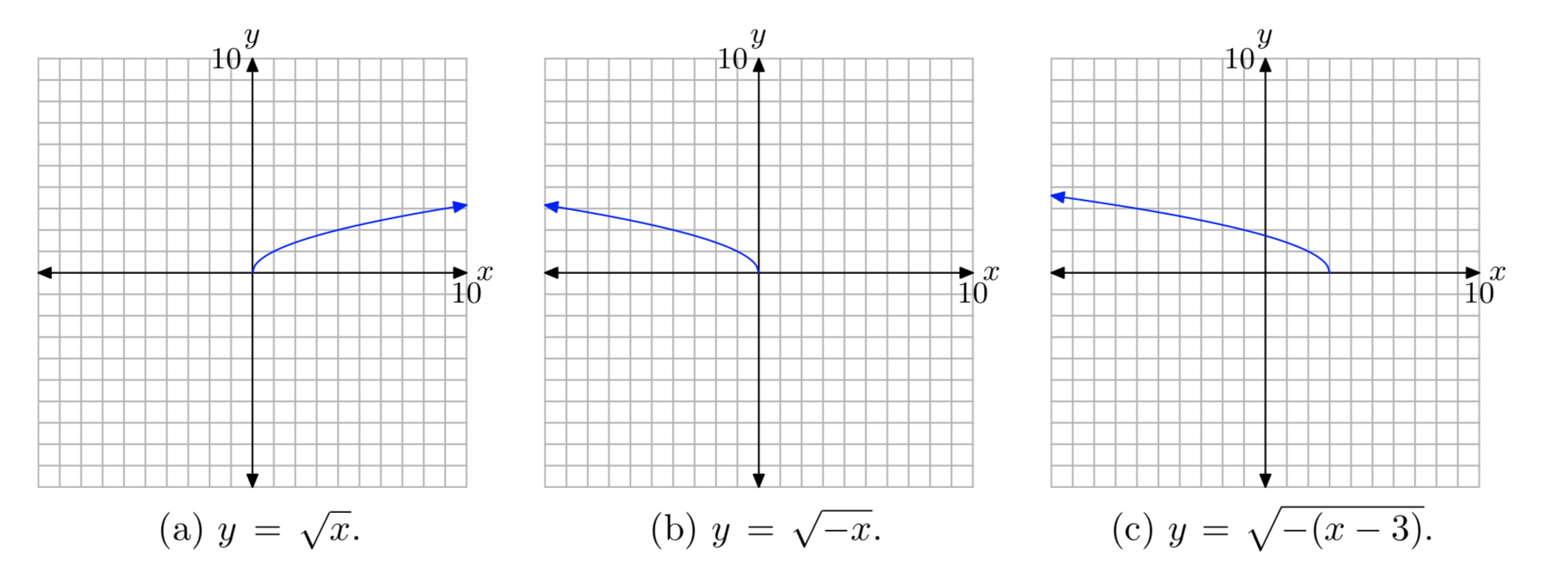



9 1 The Square Root Function Mathematics Libretexts
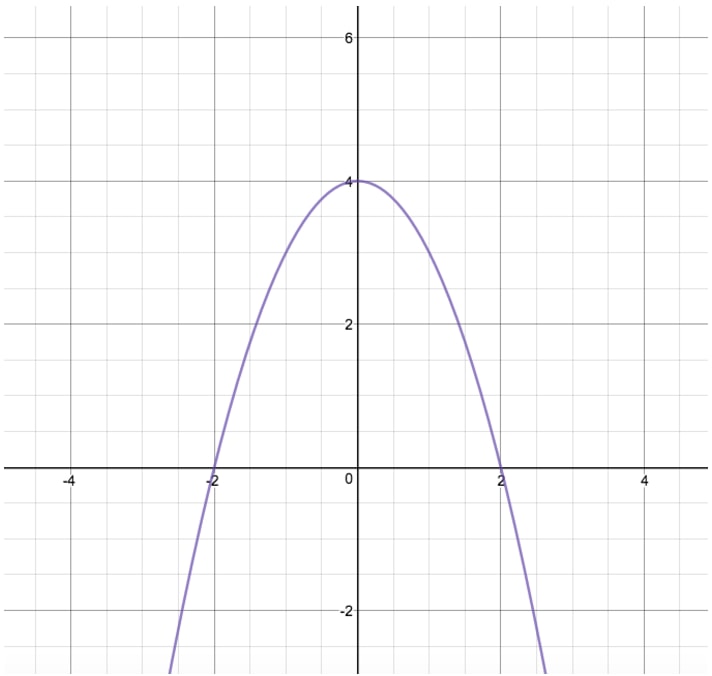
The reflection of such a parabola over the x axis is simply written as y = (x ^2) In other words, the function of f (x) becomes f (x) when reflected over the x axisA function f f is called an even function if f(x)= f(−x) f ( x) = f ( − x) for all x x in the domain of f f In other words, a function is even if performing a reflection about the y y axis does not change the graph of the function To help remember the definition of an even function, notice that the example of an even function we gaveThe parabola y=x2 2y=x 2 y, equals, x, start superscript, 2, end superscript is reflected across the xxxaxis and then scaled vertically by a factor of 4/3 3 4 start fraction, 4, divided by, 3, end fraction Reply to bhbond's post "The parabola y=x2 2y=x 2 y, equals, x



Linear Reflections Across X And Y Axis Example Youtube



How To Reflect A Graph Through The X Axis Studypug
Reflecting Functions Vertically or Horizontally Two types of transformations act like reflections or flips One transformation changes all positive outputs to negative and all negative outputs to positive The other reverses the inputs — positive to negative and negative to positive Reflecting downward puts all the points below the x axisInvariant Points) Mathematics explained in detail by experts to help students prepare for their ICSE exams



Reflection Across The X And Y Axis Youtube



How To Reflect A Graph Through The X Axis Studypug




How To Reflect Quadratic Equations Video Lesson Transcript Study Com



Parabola Parent Function Mathbitsnotebook A1 Ccss Math



How To Reflect A Graph Through The X Axis Studypug



Reflection Of A Point In X Axis Reflection Of A Point Reflection
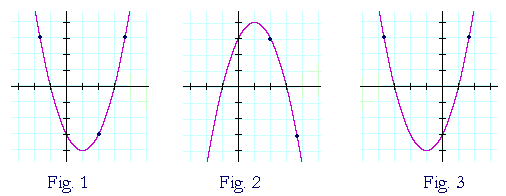



Reflections Of A Graph Topics In Precalculus



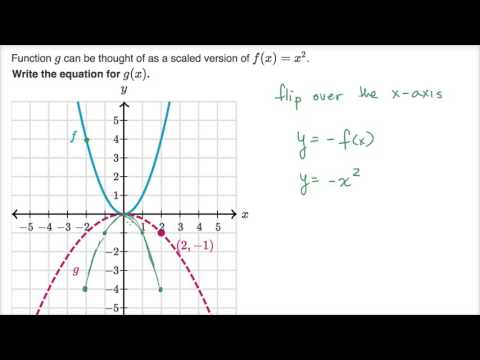
How To Reflect A Graph Through The X Axis Y Axis Or Origin



Scaling Reflecting Parabolas Video Khan Academy




Content Transformations Of The Parabola



How To Reflect Quadratic Equations Video Lesson Transcript Study Com




The Transformation Of The Graph Of A Quadratic Equation Matherudition Professional Webpage The Angry Banana Steve On Facebook Steve On Youtube The Transformation Of The Graph Of A Quadratic Equation Fundamentals Of Graph Transformations We




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Biomath Transformation Of Graphs



Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download



Harper Gallery Y Axis Chart




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
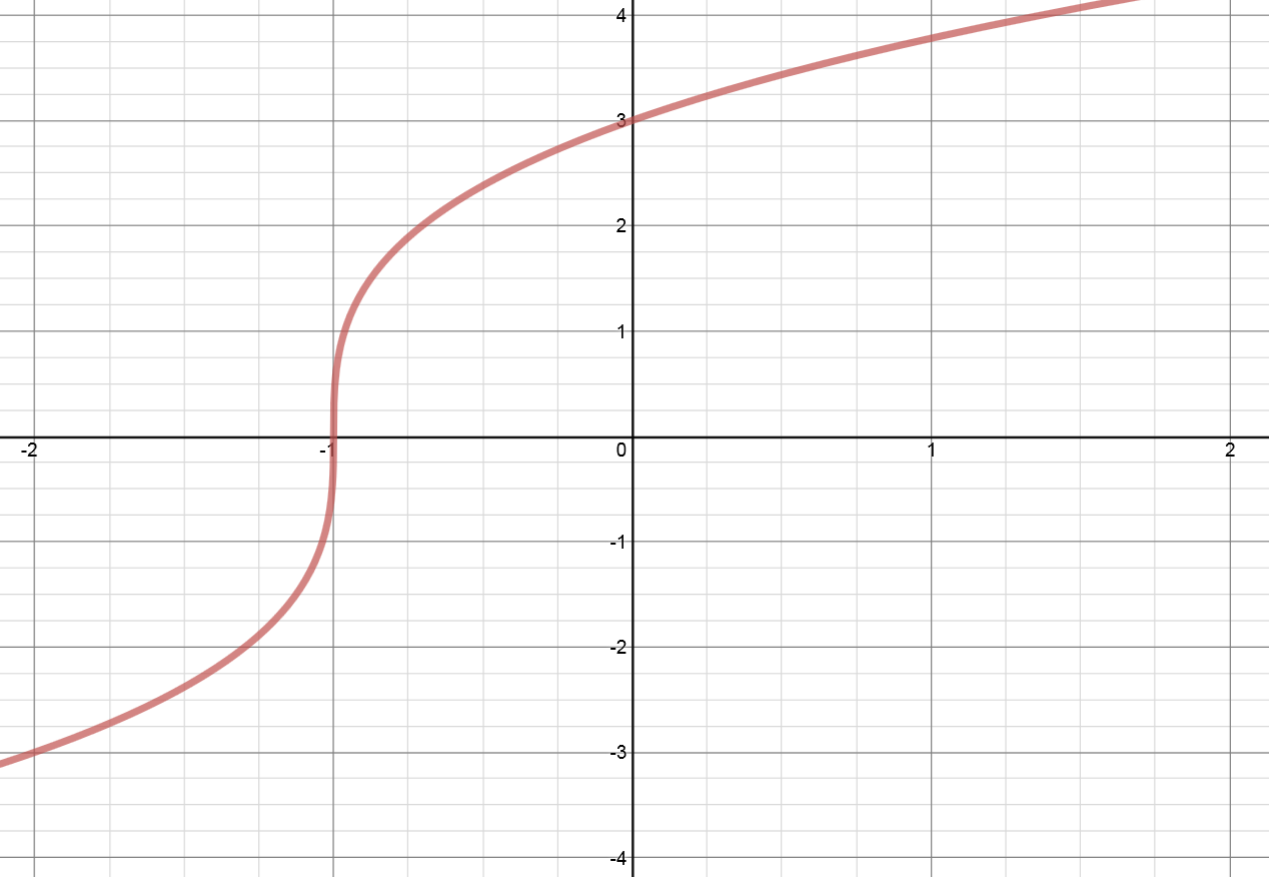



How To Reflect A Graph Through The X Axis Studypug



Solution What Is The Equation Of The Curve Y X 3 After It Is Reflected In The X Axis




Graphing Reflecting Functions Study Com




Graphing Reflecting Functions Study Com




Reflecting Functions Examples Video Khan Academy




Reflection Rules How To W 25 Step By Step Examples



A Review Of Logarithms



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflecting Shapes Video Reflections Khan Academy




Transformations Boundless Algebra



Operations On Functions Reflections And Rotations Sparknotes



Transformations Boundless Algebra



What Is The Reflection Over The Y Axis Of The Point 4 7 Quora



Parabola Parent Function Mathbitsnotebook A1 Ccss Math



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection Transformation Matrix



1



Ch 3 4
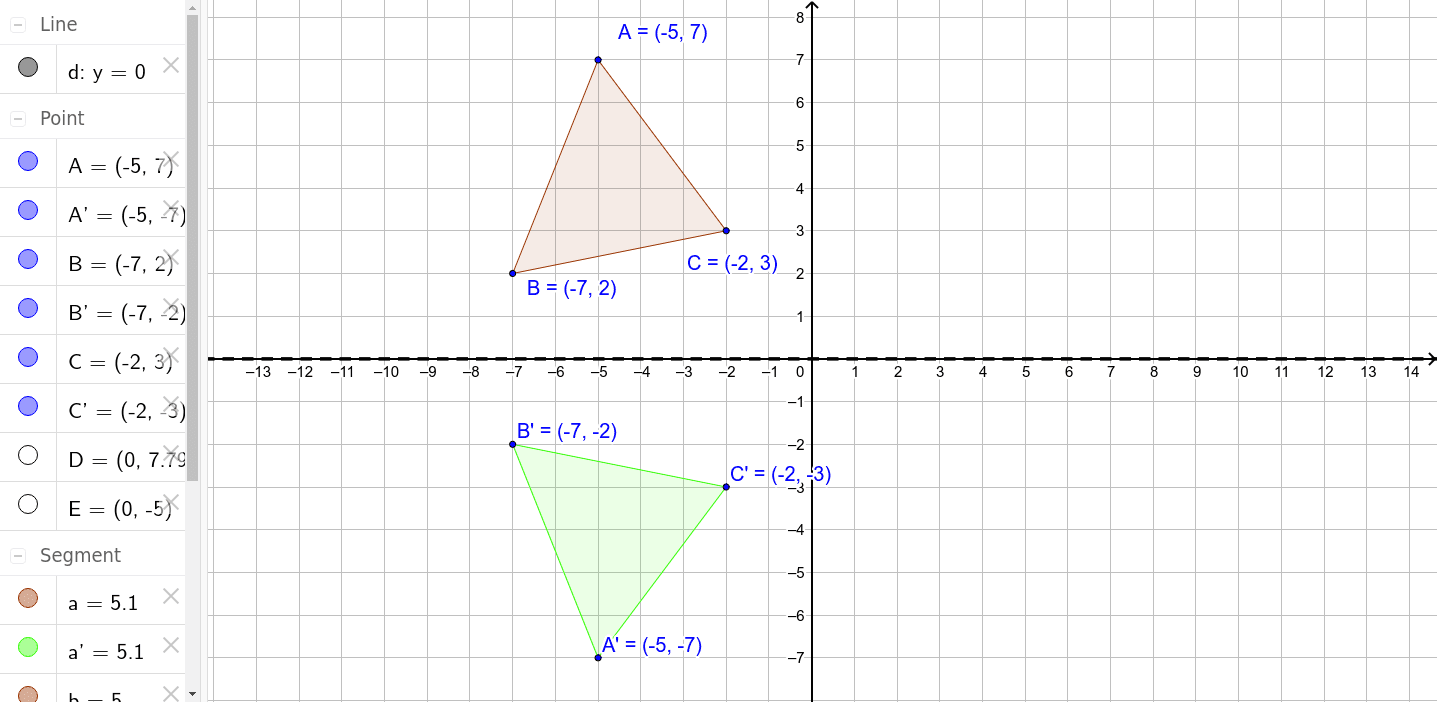



Reflection Over X Axis Geogebra
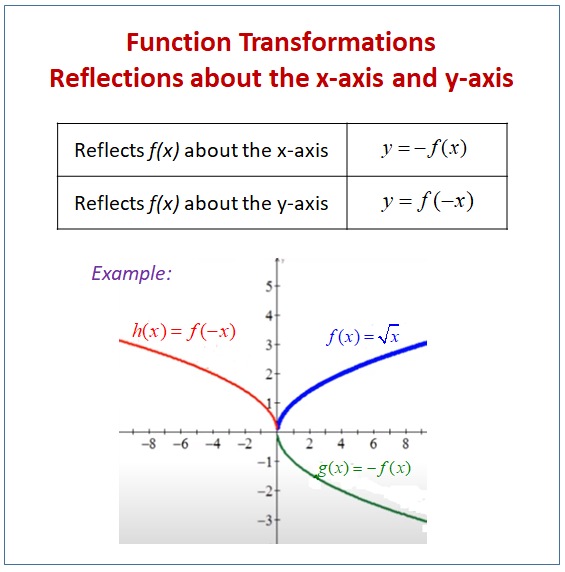



Reflecting Functions Or Graphs Examples Solutions Worksheets Videos Games Activities
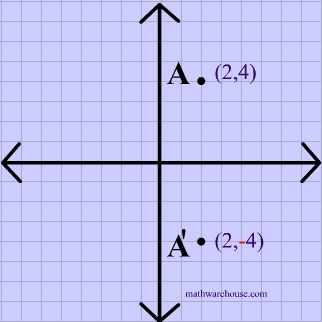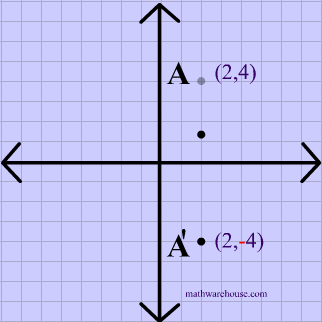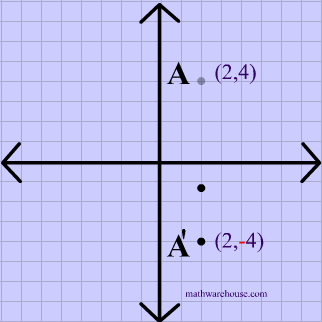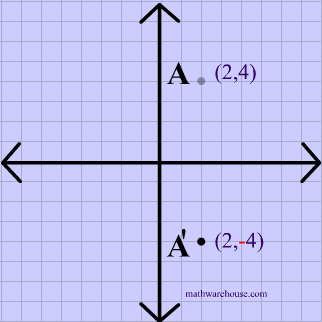



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
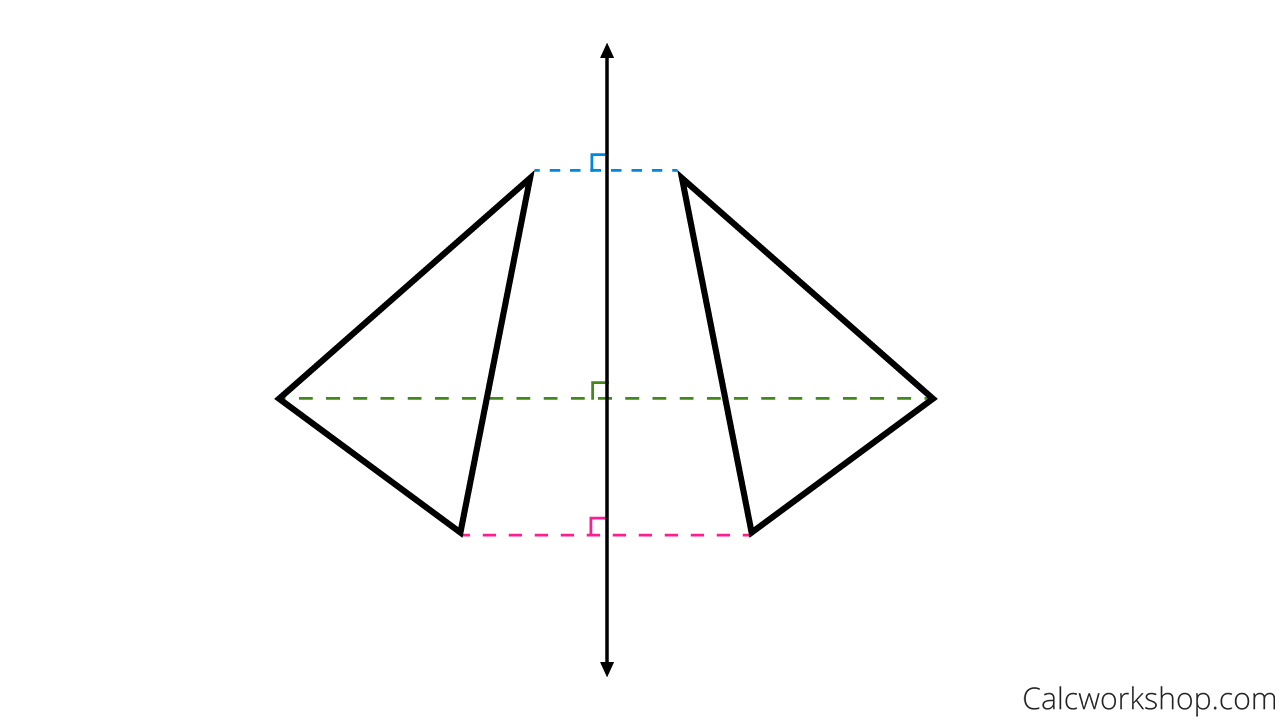



Reflection Rules How To W 25 Step By Step Examples
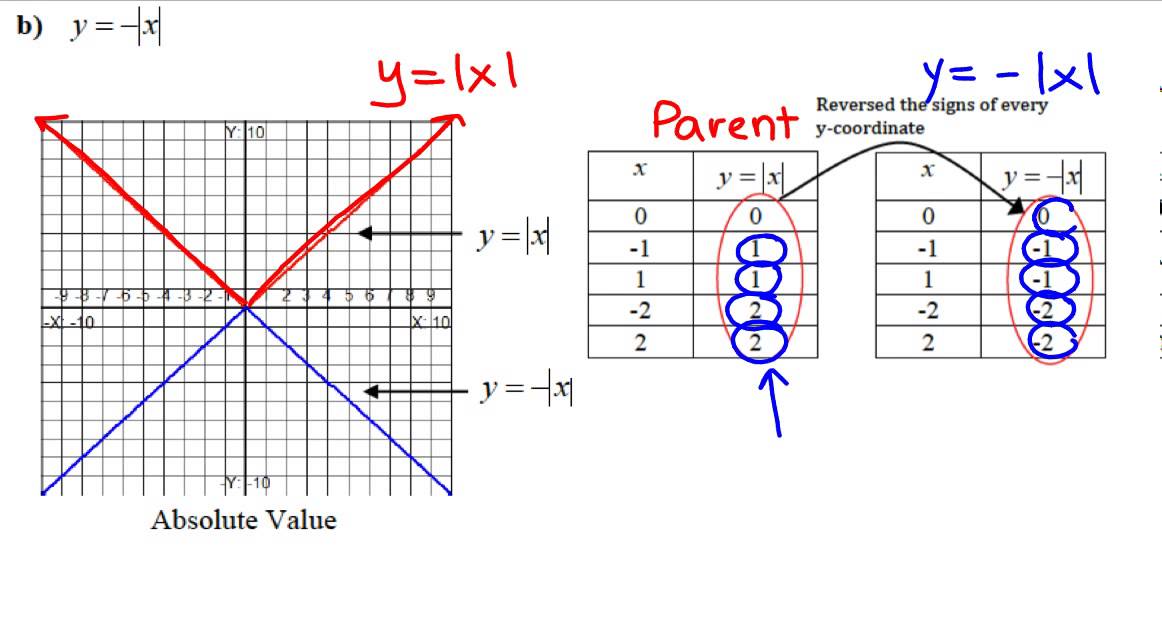



Transformations Of Reflections About The X And Y Axis Youtube



Transformations Ib Math Stuff




Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download
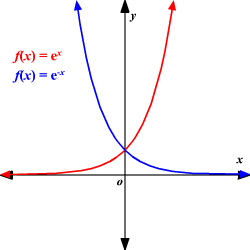



Transformation Of Function



Transformations Of Functions Mathbitsnotebook A1 Ccss Math
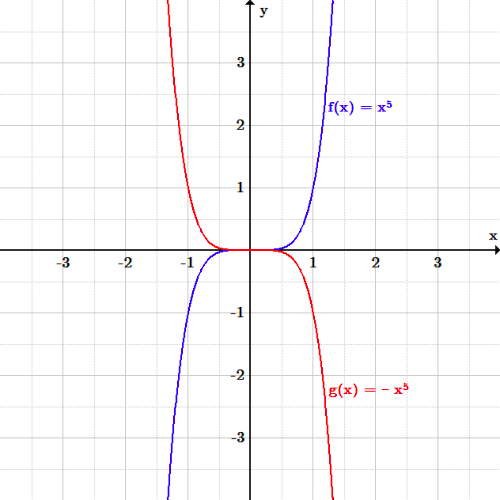



Transformations Boundless Algebra
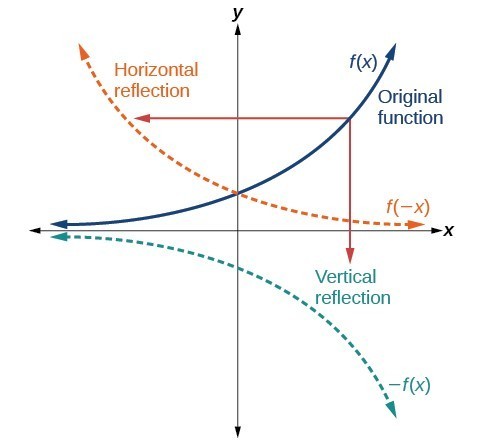



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra




How To Reflect A Graph Through The X Axis Y Axis Or Origin




The Transformation Of The Graph Of A Quadratic Equation Matherudition



Parabola Scalings And Translations Zona Land Education
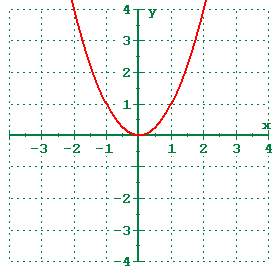



1 5 Shifting Reflecting And Stretching Graphs
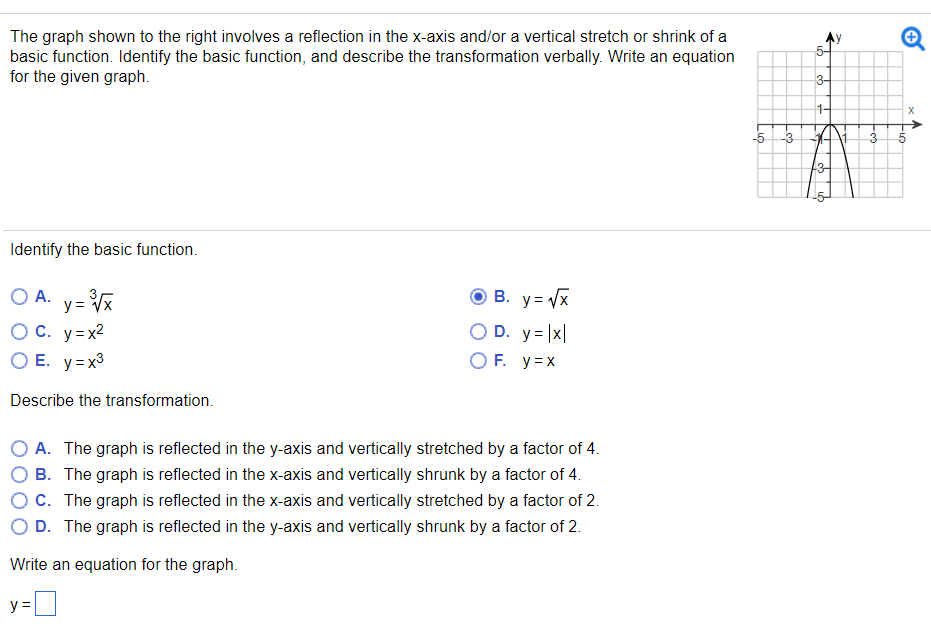



The Graph Shown To The Right Involves A Reflection In Chegg Com



1



2 02 0 Reflection Over X Axis Mov Youtube




Scaling Reflecting Parabolas Video Khan Academy



Transformation Reflection Over The X Axis Youtube
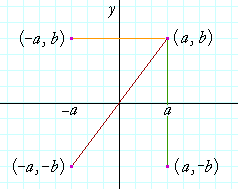



Reflections Of A Graph Topics In Precalculus




Your Transformation Equation Y A F X H K A X Axis Reflection A 1 Vertical Stretch 0 A College Algebra Teaching Math Middle School Math



Assignment 2 Transforming Parabolas



Graphs Of Exponential Functions
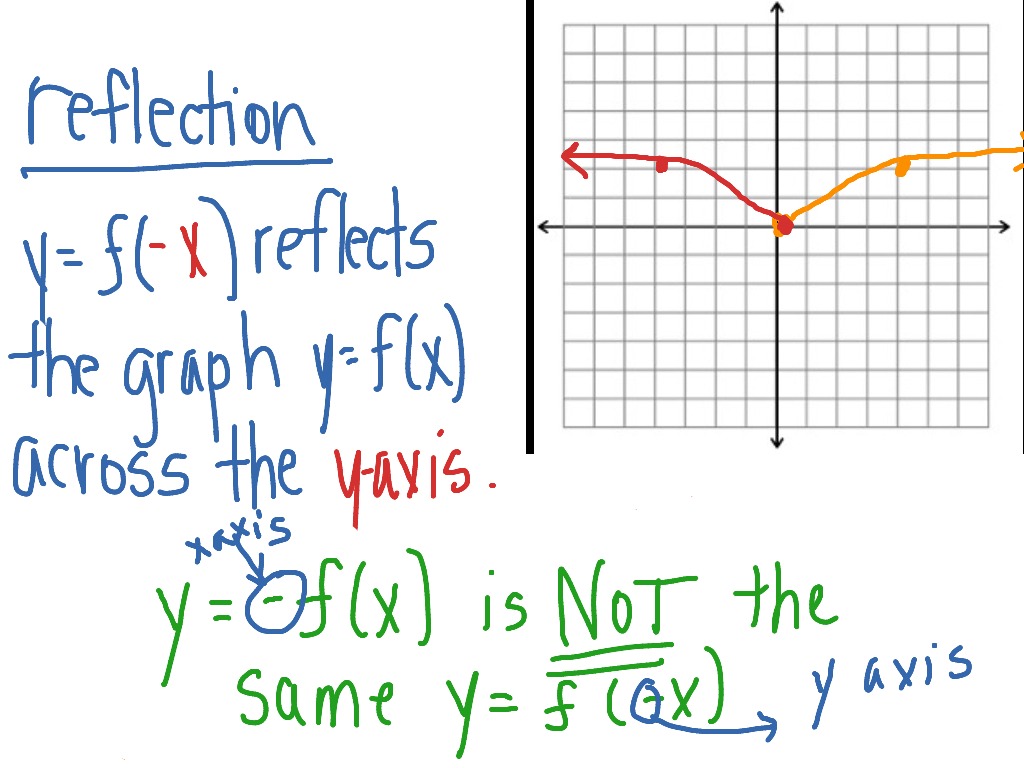



Reflection Across The Y Axis Math Functions Showme
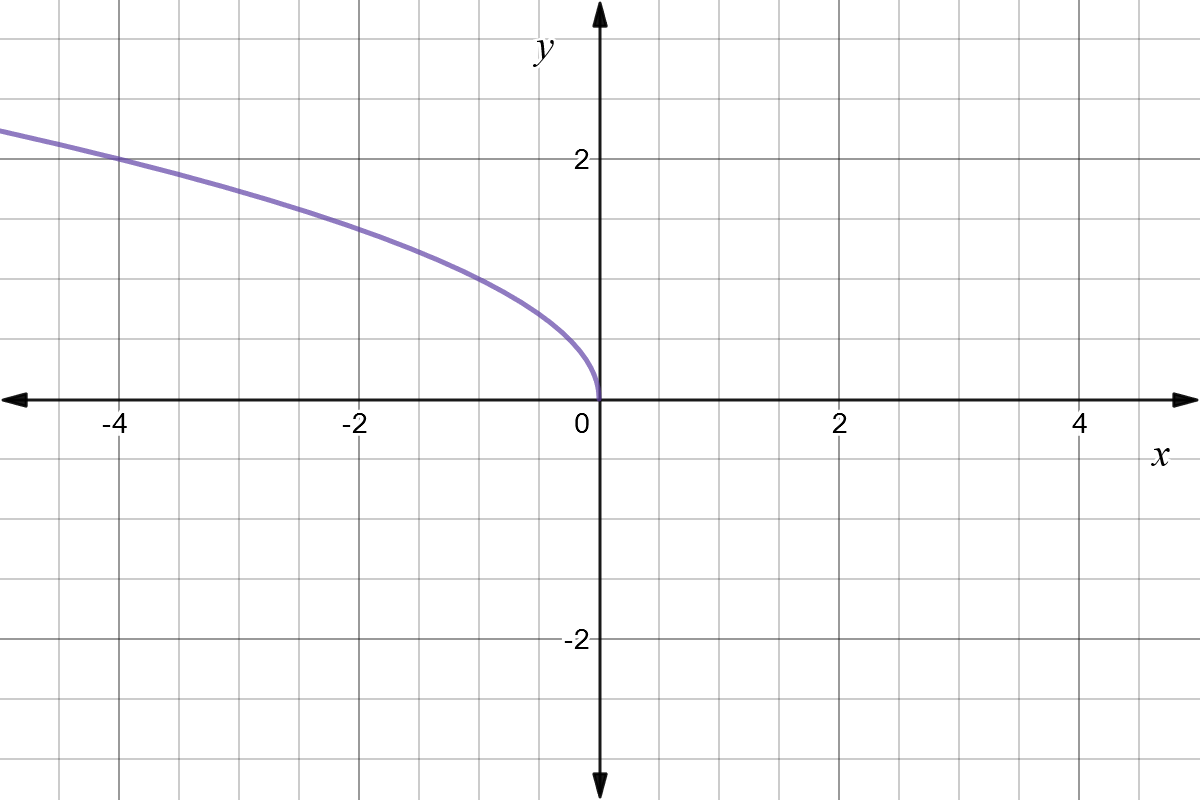



Reflect Function About Y Axis F X Expii
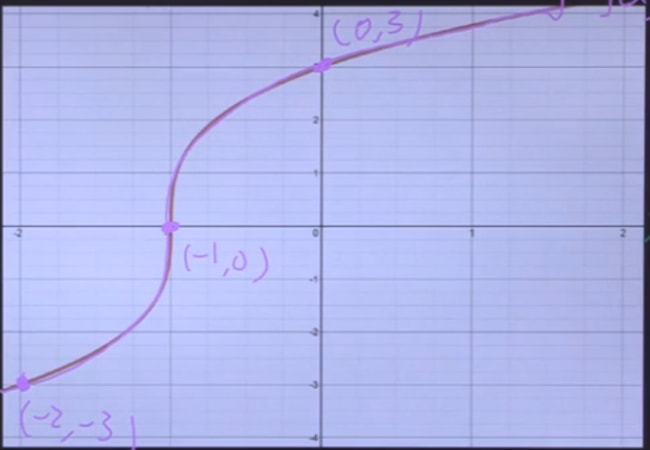



How To Reflect A Graph Through The X Axis Studypug




Reflect Function About Y Axis F X Expii




How To Reflect A Graph Through The X Axis Y Axis Or Origin
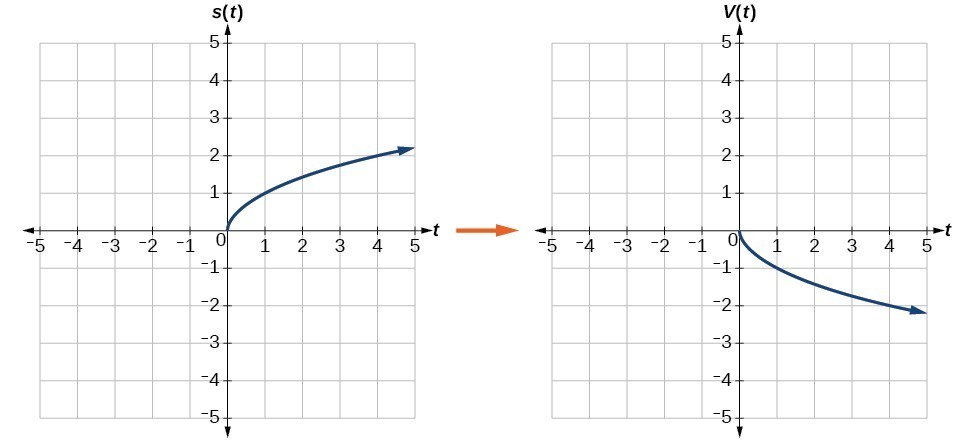



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
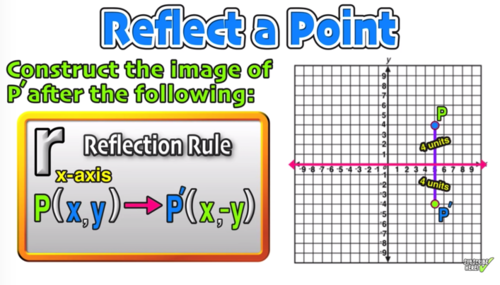



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation




Using Transformations To Graph Functions



Assignment 2 Transforming Parabolas
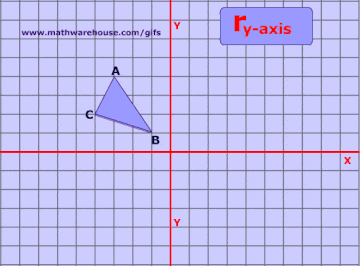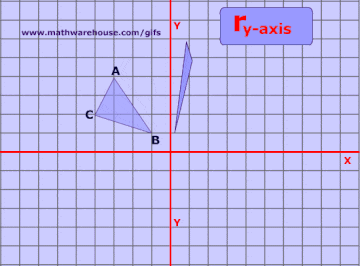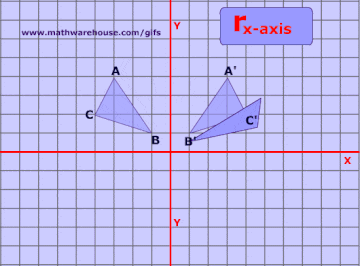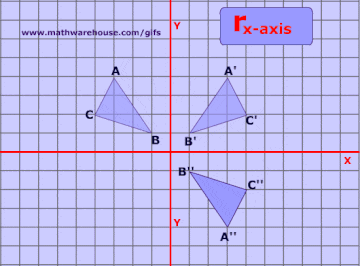



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
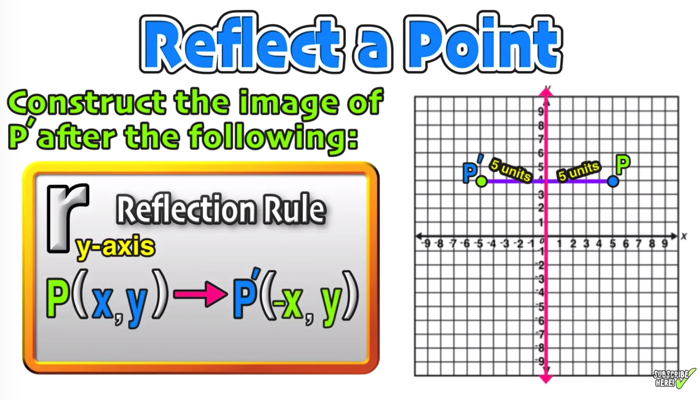



Reflection Over The X And Y Axis The Complete Guide Mashup Math
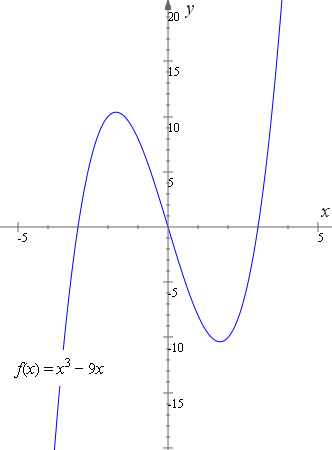



How To Reflect A Graph Through The X Axis Y Axis Or Origin
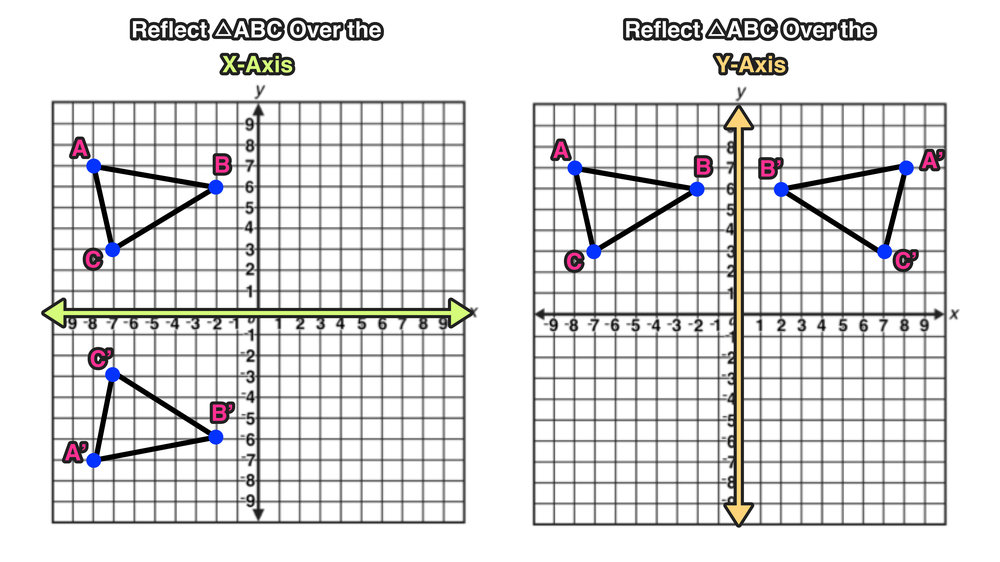



Reflection Over The X And Y Axis The Complete Guide Mashup Math



How To Reflect A Graph Through The X Axis Y Axis Or Origin
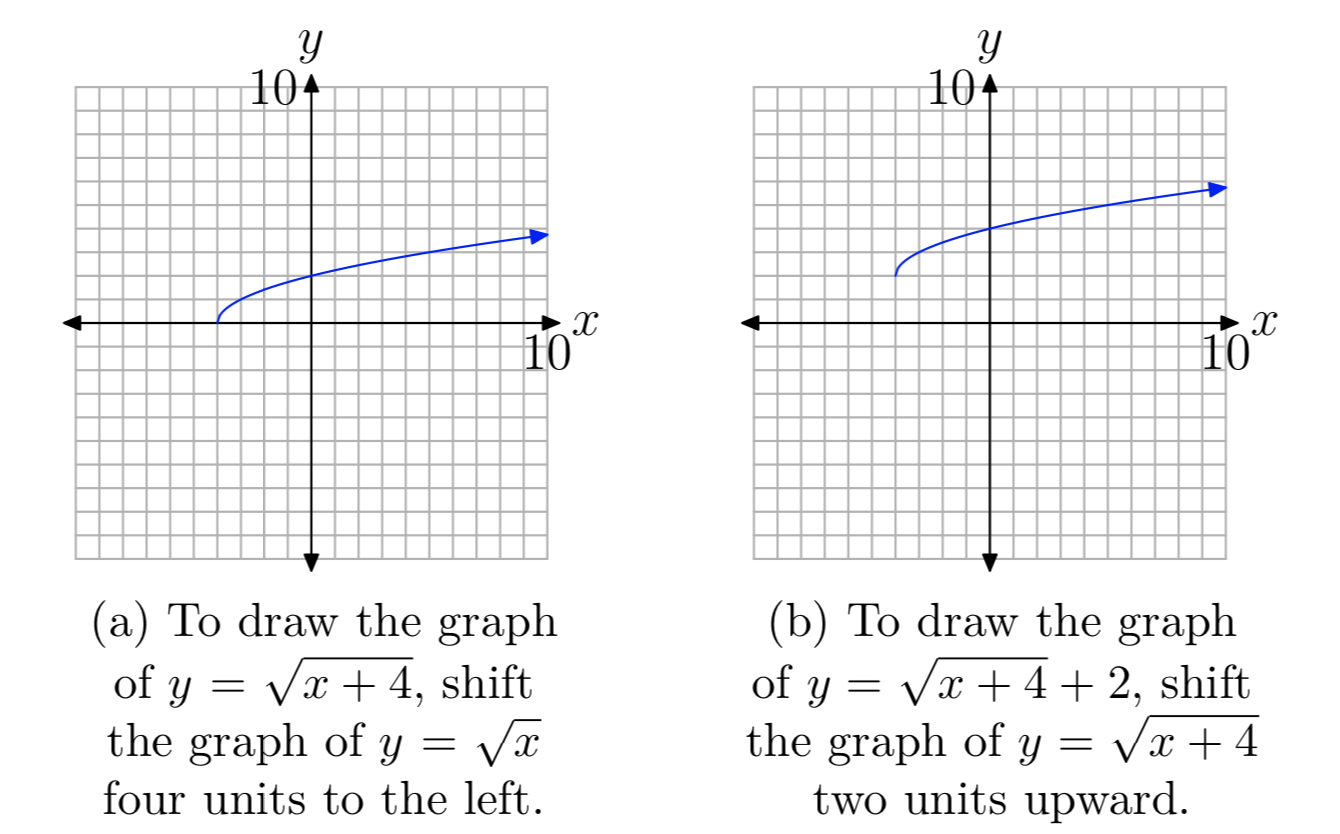



9 1 The Square Root Function Mathematics Libretexts




Reflections



0 件のコメント:
コメントを投稿